Intersection of line segments using complex variables in Matlab

NOTE: Sep. 2, 2011, this is a substantial edit of my previous post to explain more details.

A post by Loren Shure of Mathworks, reminded me of a function, PolylineIntersectSegment.m, that I wrote to compute the intersection of a polyline with a line segment. This function nicely combines the topics of my last two posts, use of complex variables as vectors and lines, so I will discuss it in more detail. The use of complex variables simplifies the code and makes it easier to understand and modify.

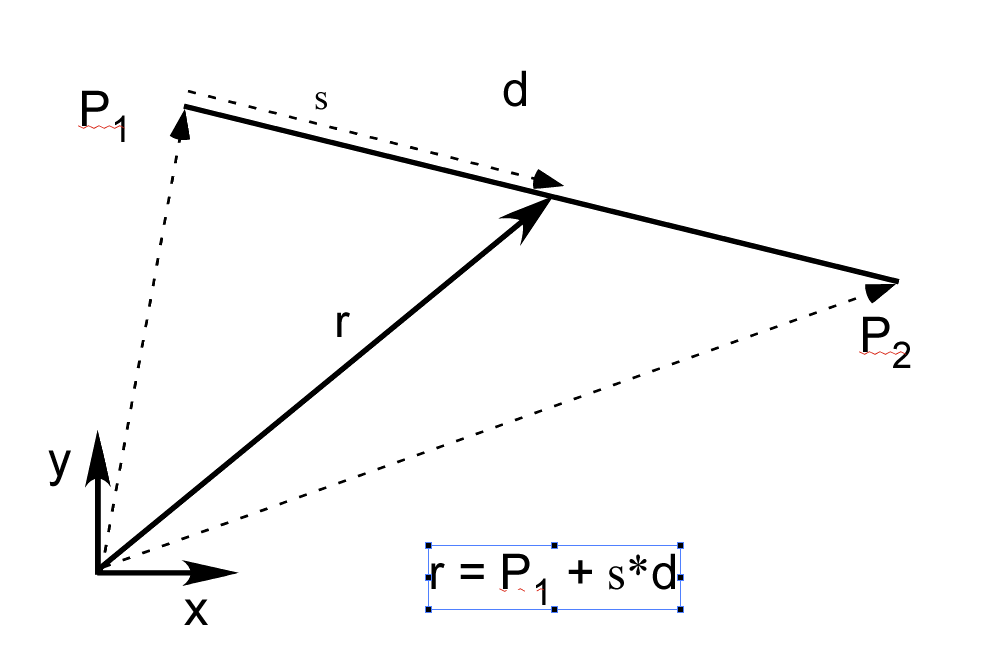
A polyline[1] is a set of connected line segments. Line segments are naturally specified by their start and end points instead of the n and ŝ vectors described in my last post. An example is shown in Fig. 1↓

Figure 1 A line segment is specified by its start and end points, P₁, P₂. From these, we can compute the difference vector d = P₁ − P₂ and a point on the line segment is r = P₁ + sd 0 ≤ s < 1.

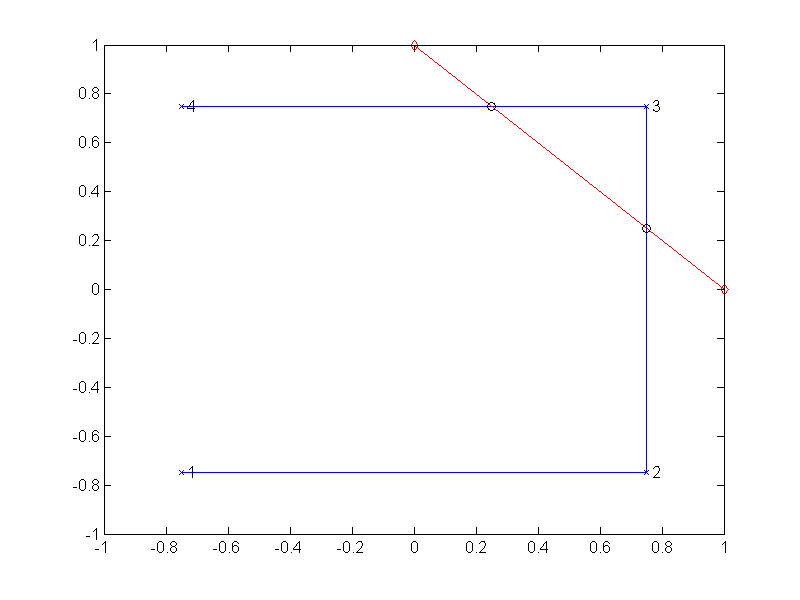
In a polyline, as shown in Fig. 3↓, the end point of one segment is the start point of the next. The four points (1 − 4) define a three segment polyline (shown in blue). A polyline is in general not closed although it can be. In addition, the segments of the polyline can cross.

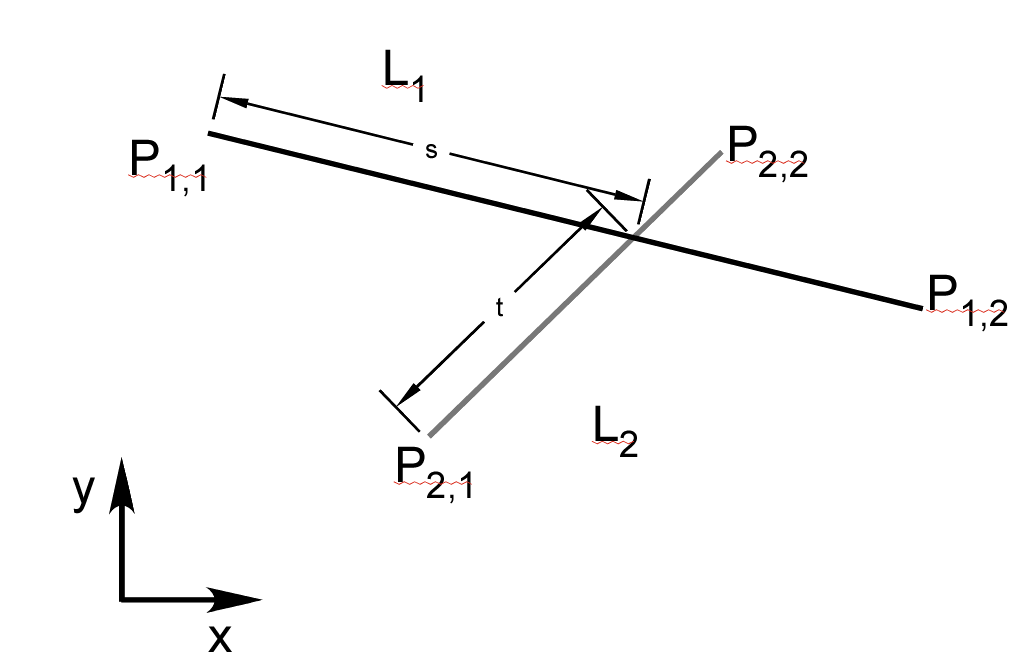
The PolylineIntersectSegment.m function code is based on the intersection between two segments L₁ and L₂ determined by their end points (see Fig. 2↓)

L₁: P₁₁, P₁₂ L₂: P₂₁, P₂₂ .

Letting the vectors d_k = P_k2 − P_k1, k = 1, 2 be the vectors from the start to the end points of the two segments, points on the segments are r₁ = P₁₁ + sd₁ and r₂ = P₂₁ + td₂ with 0 ≤ s < 1 and 0 ≤ t < 1. At the point of intersection, r₁ and r₂ are equal

r₁ = P₁₁ + sd₁ = r₂ = P₂₁ + td₂

Rearranging terms

(1) sd₁ − td₂ = P₂₁ − P₁₁ = D.

Figure 2 Intersection of two line segments.

Now let n_k be vectors perpendicular to d_k, k = 1, 2. If we use complex numbers to represent the vectors, we can compute the perpendicular vectors by multiplying by e^{iπ ⁄ 2} = i so n_k = id_k. Taking the dot product of both sides of Eq. 1↑, we can solve for s_int and t_int. Dotting first with n₂ and solving

s_int = (D⋅n₂)/(d₁⋅n₂)

and then with n₁

t_int = − (D⋅n₁)/(d₂⋅n₁).

We can then test that 0 ≤ s < 1 and 0 ≤ t < 1 for intersection points. I use open intervals to avoid duplicate hits when segments intersect at end points. You can change this test depending on how inclusive you want to make your definition of intersection to be. This will depend on your application so I do not think there is a single correct answer. The test in the code is shown below and it easy to change. If the segments are parallel or have zero length, then there will be a division by zero. Matlab will return a NaN for s_int or t_int and the logical test will return false indicating no intersection. You can also modify the code to test for these and do something different.

% test for intersection in PolylineIntersectSegment
intersectsOK = (s>=0)&(s<1)&(t>=0)&(t<1);

The actual point of intersection will be

P_intersect = P₁₁ + s_intd₁

The code of PolylineIntersectSegment.m (see the zip file for this post) shows how the use of complex variables simplifies things. As noted above, to find a perpendicular vector, multiply the vector by i, which rotates it by 90 degrees. All the Matlab functions like diff work with complex variables. The code is a straightforward implementation of the equations. Some examples are given with the zip file and are shown in the box. The polyline in the third example is shown in Fig. 3↓.

Figure 3 Example of intersection of a line segment and a polyline. The test segment is in red, the polyline in blue with vertexes numbered, and the intersection points are circles.

%%  intersect of 2 lines
zseg = [0 1i]; % line along the y axis
p1 = [-.5 .5] + 0.5*1i; % line segment parallel to x-axis at y=0.5
zi = PolylineIntersectSegment(zseg,p1);
disp(zi)

%% add another segment along same direction as first one but of zero length
% only chooses the intersection with the correct segment
p1null = [p1, p1(end)];
zi = PolylineIntersectSegment(zseg,p1null);
disp(zi)

%% add another segment along same direction as first one
% only chooses the intersection with the correct segment
p2 = [p1, (1.5+0.5i)];
zi = PolylineIntersectSegment(zseg,p2);
disp(zi)

%% add segment parallel to test segment in y-direction
% ignores segments to test segment
p3 = [p2,(1.5+2i)];
zi = PolylineIntersectSegment(zseg,p3);
disp(zi)

%% display results
fh = figure;
plot(p3,’-xb’)
hold on
plot(zseg,’-rd’)
plot(zi,’ok’)
hold off
axis([-2 2 -2 2])

The code uses the zdot function for the dot product of two vectors represented as complex variables.

function d = zdot(z1,z2) % dot product for complex vectors
     d = real( z1(:) .* conj(z2(:)));

Last edited Sep. 1, 2011

Linking is allowed but reposting or mirroring is expressly forbidden.

References

[1] Philip Schneider, David H. Eberly: Geometric Tools for Computer Graphics. Morgan Kaufmann, 2002.