aprendtech.com >> blog >> this post

If you have trouble viewing this, try the pdf of this post. You can download the code used to produce the figures in this post.

The NKQ detector

The NKQ detector introduced in my paper[1] is a generalization of the NQ where instead of just counting the photons we use pulse height analysis (PHA) to separate the photons into K bins depending on their energies and simultaneously measure their total energy. This gives performance similar to PHA with the number of bins plus one so it may be easier to implement. As with the NQ detector, the integrated energy Q can be used in regions where high count rate leads to excessive pulse pileup.

Covariance of NKQ Detector Measurements

With no pulse pileup, the numbers of photons in the individual PHA bins, {N₁, N₂, …N_K}, are independent Poisson random variables with parameters λ_k, k = 1…K. The total number of photons, N, is the sum

N = ^K⎲⎳_k = 1N_k.

Since the sum of independent Poisson random variables is also a Poisson random variable with parameter equal to the sum of the parameters of the terms, N is Poisson with parameter

λ = ^K⎲⎳_k = 1λ_k.

The NKQ detector also measures the total energy Q of all the photons.

The mean value vector of the measurements is

⟨⎡⎢⎢⎢⎢⎢⎢⎢⎣ N₁ N₂ ⋯ N_K Q ⎤⎥⎥⎥⎥⎥⎥⎥⎦⟩ = ⎡⎢⎢⎢⎢⎢⎢⎢⎣ λ₁ λ₂ ⋯ λ_K λ⟨E⟩ ⎤⎥⎥⎥⎥⎥⎥⎥⎦.

To derive the joint statistics, we only need to consider the two bin case and derive the results for cov(N₁, Q). These results can be immediately generalized to the K bin case because, from the point of view of the analysis, all the other measurements can be summed to a single Poisson random variable that is independent of N₁,so is equivalent to the two bin case. Also, without loss of generality, the results for N₁ are applicable to any of the other individual measurements. The covariance of N₁ and Q is defined as

(1) cov(N₁, Q) = ⟨(N₁ − < N₁ > )(Q − < Q > )⟩.

Expanding the product

(2) cov(N₁, Q) = ⟨N₁Q⟩ − < N₁ > < Q > .

Expanding the first term

(3) ⟨N₁Q⟩ = ⟨⟨N₁Q⟩|_N₁ = n⟩ = ^∞⎲⎳_n₂ = 0^∞⎲⎳_n₁ = 0n₁⟨^n₁⎲⎳_i = 1E_i + ^n₂⎲⎳_i = 1E_i⟩Prob{N₁ = n₁}Prob{N₂ = n₂}.

The E random variables have same probability distribution so

⟨^n₁⎲⎳_i = 1E_i⟩ = n₁⟨E⟩₁

where ⟨E⟩₁ denotes the mean value of the instances of E in the first bin. Similarly

⟨^n₂⎲⎳_i = 1E_i⟩ = n₂⟨E⟩₂.

Substituting in (3↑)

⟨N₁Q⟩ = ^∞⎲⎳_n₂ = 0^∞⎲⎳_n₁ = 0 [n²₁⟨E⟩₁ + n₁n₂⟨E⟩₂]Prob{N₁ = n₁}Prob{N₂ = n₂}

⟨N₁Q⟩ = ⟨N²₁⟩⟨E⟩₁ + λ₁λ₂⟨E⟩₂

where the last step uses the fact that N₁ and N₂ are independent. The second moment of a Poisson random variable is

⟨N²₁⟩ = λ²₁ + λ₁.

The final result for the first term in (2↑) is

⟨N₁Q⟩ = (λ²₁ + λ₁)⟨E⟩₁ + λ₁λ₂⟨E⟩₂

In the second term in (2↑), < N₁ > = λ₁ and < Q > = (λ₁ + λ₂)⟨E⟩. The overall mean value ⟨E⟩ can be expressed in terms of the bin mean values as

⟨E⟩ = (λ₁⟨E⟩₁ + λ₂⟨E⟩₂)/(λ₁ + λ₂)

so the second term is

< N₁ > < Q > = λ²₁⟨E⟩₁ + λ₁λ₂⟨E⟩₂.

Combining the first and second terms gives the final result

cov(N₁, Q) = λ₁⟨E⟩₁.

By the argument stated above, this can be generalized to

cov(N_k, Q) = λ_k⟨E⟩_k.

As previously derived the variance of Q is σ²_Q = λ⟨E²⟩, so the covariance matrix is

(4) Cov({N_k, k = 1…K}, Q) = ⎡⎢⎢⎢⎢⎢⎢⎢⎣ λ₁ 0 0 0 λ₁⟨E⟩₁ 0 λ₂ 0 0 λ₂⟨E⟩₂ 0 0 ⋯ ⋯ ⋯ 0 0 ⋯ λ_K λ_K⟨E⟩_K λ₁⟨E⟩₁ λ₂⟨E⟩₂ ⋯ λ_K⟨E⟩_K λ⟨E²⟩ ⎤⎥⎥⎥⎥⎥⎥⎥⎦.

Covariance of logarithm of NKQ measurements

The same arguments used in the previous section are also applicable to the logarithms of the measurements, so I will derive the covariance of log(N₁) and log(Q) for the two group case. Using the general result

cov[log(N₁), log(Q)] = ⟨log(N₁)log(Q)⟩ − ⟨log(N₁)⟩⟨log(Q)⟩.

As with the derivation for the NQ detector, the first term is

⟨log(N₁)log(Q)⟩ ≈ log[⟨N⟩]log[⟨Q⟩] + (cov(N₁, Q))/(⟨N₁⟩⟨Q⟩).

Inserting the results from the previous section

(cov(N₁, Q))/(⟨N₁⟩⟨Q⟩) = (⟨E⟩₁)/(⟨Q⟩).

Combining these

cov[log(N₁), log(Q)] = (⟨E⟩₁)/(⟨Q⟩)

Using the result from the NQ detector for the variance of log(Q) and recalling that F = (⟨E²⟩)/(⟨E⟩²) and ⟨Q⟩ = λ⟨E⟩, the covariance matrix is

Cov({log(N_k), k = 1…K}, log(Q)) = (1)/(λ)⎡⎢⎢⎢⎢⎢⎢⎢⎣ λ ⁄ λ₁ 0 ⋯ 0 (⟨E⟩₁)/(⟨E⟩) 0 λ ⁄ λ₂ 0 0 (⟨E⟩₂)/(⟨E⟩) 0 0 ⋯ 0 ⋮ 0 0 0 λ ⁄ λ_K (⟨E⟩_K)/(⟨E⟩) (⟨E⟩₁)/(⟨E⟩) (⟨E⟩₂)/(⟨E⟩) ⋯ (⟨E⟩_K)/(⟨E⟩) F ⎤⎥⎥⎥⎥⎥⎥⎥⎦.

Monte Carlo simulation of N2Q statistics

The code for this post shows how to generate Fig. 1↓, which compares the N2Q covariance and correlation with the theoretical results in Eq. 1↓. These quantities are plotted versus the inter-bin separation energy of the two bin PHA. Note that the correlation (and covariance) of the counts with Q increases for N₁ but decreases for N₂ as the threshold energy increases.

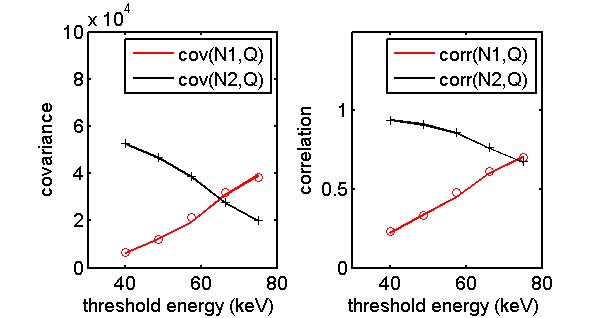
Figure 1 N2Q statistics. Shown are both the covariance and the correlation of the two photons counts and the total energy. The solid lines are the theoretical values from Eq. 4↑ while the symbols show the Monte Carlo values.

Conclusion

The theoretical formulas derived in this post fit the Monte Carlo simulation results. I was not able to derive simple analytical formulas for the NKQ SNR so future posts will compute it numerically and compare it to the optimal SNR with complete information and also to other types of detectors.

Last editedDec 06, 2012

Linking is allowed but reposting or mirroring is expressly forbidden.

References

[1] Robert E. Alvarez: “Near optimal energy selective x-ray imaging system performance with simple detectors”, Med. Phys., pp. 822—841, 2010.