Intersection of curves

In this post, I extend my PolylineIntersectSegment post to find all the intersections between two polylines. We can use the code to find the intersection of two curves by approximating them as polylines. The code is fast so you can use small intervals to get accurate results. Again, the use of complex variables makes the code easier to understand and modify.

The algorithm is implemented in the PolylineIntersectPolyline.m function. The code, without the help section, is listed in the box

function zi_all = PolylineIntersectPolyline(pline1,pline2)
    % test number of lines segments in polyline
pline1 = pline1(:);    
nseg1 =  numel(pline1)-1;   
assert(nseg1>0);

pline2 = pline2(:);
nseg2 =  numel(pline2)-1;   
assert(nseg2>0);

    % find overlapping segments -
x1 = real(pline1); y1 = imag(pline1);
x2 = real(pline2); y2 = imag(pline2);    
[idx1,idx2] = find( ... % indexes into pline1 and pline2
    repmat(min(x1(1:end-1),x1(2:end)),1,nseg2) <= ...
	repmat(max(x2(1:end-1),x2(2:end)).’,nseg1,1) & ...
	repmat(max(x1(1:end-1),x1(2:end)),1,nseg2) >= ...
	repmat(min(x2(1:end-1),x2(2:end)).’,nseg1,1) & ...
	repmat(min(y1(1:end-1),y1(2:end)),1,nseg2) <= ...
	repmat(max(y2(1:end-1),y2(2:end)).’,nseg1,1) & ...
	repmat(max(y1(1:end-1),y1(2:end)),1,nseg2) >= ...
	repmat(min(y2(1:end-1),y2(2:end)).’,nseg1,1) ...
    );
     
   % find all pairwise intersections
zi_all = [];

for k  = 1:numel(idx1)
  zi = PolylineIntersectSegment([pline1(idx1(k)),pline1(idx1(k)+1)], ...
   [pline2(idx2(k)),pline2(idx2(k)+1)]);
  zi_all = [zi_all; zi(:)];
end

The test for overlapping segments speeds up the function since otherwise we would have to make a call to PolylineIntersectSegment for every point in the one of the polylines. I used the code from the intersections function in the Mathworks File Exchange. The test determines whether the rectangular boxes enclosing two segments overlap. If they do not, then the segments cannot intersect. So, we only have to test the overlapping boxes, which is usually much fewer than the product of the number of segments in the two polylines.

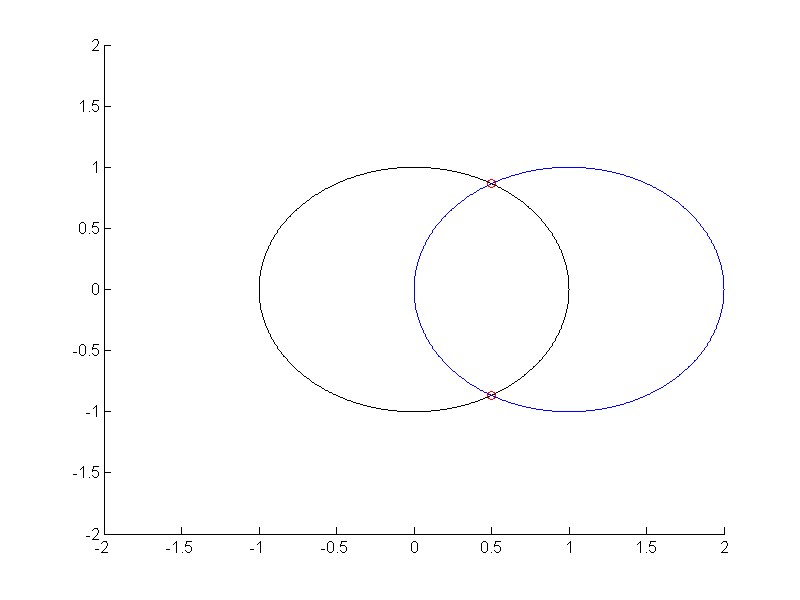
Code to test the function is shown in the box below. The result is plotted in Fig. 1↓.

%%  create 2 polylines and intersect them
% the polylines are circles with different centers
npnts = 1000;
p1 = exp(1i*linspace(0,2*pi,npnts)) ; % hexagon, radius 1, centered at origin
p2 = exp(1i*linspace(0,2*pi,npnts)) + 1; % square centered at x = 1
tic
zi = PolylineIntersectPolyline(p1,p2);
dt_2 = toc;
fprintf(1,’PolylineIntersectPolyline took %.2f seconds for %.0f line segments...\n’,dt_2,npnts-1);

Figure 1 Example of using PolylineIntersectPolyline to find the intersection of two circles. The code is shown in the box. The intersections are the small red circles.

edit: I gave some thought to the test for overlapping segments that I mentioned in the PolylineIntersectSegment post. I modified the functions to add an optional parameter called allhits. If a string with this parameter is used as an input, then a more loose definition of intersection is used. The additional code in PolylineIntersectSegment is

   % the offsets to the intersections
d1_dot_n2 = zdot(d1,ns_2);   
s = zdot(Ds,ns_2)./d1_dot_n2;

d2_dot_n1 = zdot(d2,ns_1);
t = -zdot(Ds,ns_1)./d2_dot_n1;

if allhits
   intersectsOK = (s>=0)&(s<=1)&(t>=0)&(t<=1);
      % process possible parallel segments hits
   idx = find( (abs(d1_dot_n2) < eps) & (t >=0) & (t <=1)  ) ;
   intersectsOK(idx) = true;
   s(idx) = 0.5;

   idx = find( (abs(d2_dot_n1) < eps) & (s>=0) & (s<=1)  )  ;
   intersectsOK(idx) = true;
   s(idx) = 0.5;
   
else
   intersectsOK = (s>=0)&(s<1)&(t>=0)&(t<1);
end

With the looser definition, PolylineIntersectPolyline finds the intersections in the FEX meetpoint function.

%% test meetpoint data
% The output of meetpoint is:
% >> [x’ y’]
% ans =
%     0.5000 0.5000
%     1.0000 1.0000
%     1.3000 1.3000
%     2.0000 1.5000
%     4.2000 1.8000
%     5.0000 1.8000
x1=[0 1.5 3 5 5];
y1=[0 1.5 1.5 2 1];
x2=[.2 .5 .5 1 1 2 2 5 5];
y2=[.2 .5 .8 1 1.3 1.3 1.8 1.8 .5];
p1 = zcomp([x1’ y1’]);
p2 = zcomp([x2’ y2’]);
zi = PolylineIntersectPolyline(p1,p2,’allhits’)
zi =

   0.5000 + 0.5000i
   1.0000 + 1.0000i
   1.3000 + 1.3000i
   2.0000 + 1.5000i
   4.2000 + 1.8000i
   5.0000 + 1.8000i

Last edited Sep. 4, 2011

Linking is allowed but reposting or mirroring is expressly forbidden.

Intersection of curves

References