If you have trouble viewing this, try the pdf of this post. You can download the documents in this post.

A Line object--basic formulas

Computational geometry is an interesting and important topic for imaging in general and x-ray imaging in particular. In this post, I describe the basic formulas for perhaps the most fundamental geometric object—a straight line in three dimensions. The object can also be used in 2D to represent a line in an image.

I used the results described here in the code for my previous posts (here,here, and here) on a CT simulator. In particular, they used a line object. In this post I will derive the basic formulas for an object that encapsulates a three dimensional line. In following posts, I will describe C++ and Matlab implementations and show some applications.

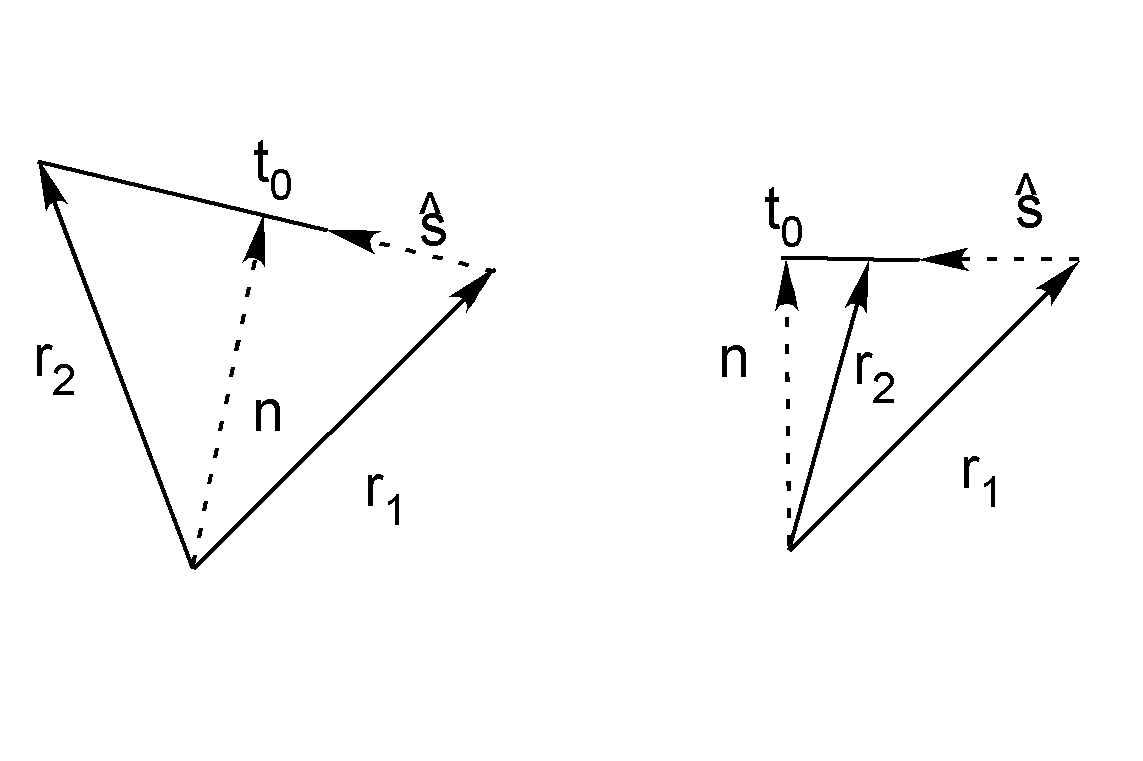
Standard books[1] specify a line by any two points on it. I prefer a more structured definition, which has substantial advantages in implementation of computations as you will see in the examples. I specify a line by two vectors: a vector n from the origin perpendicular to the line and a unit length vector direction vector ŝ along the line (see Fig. 1↓).

Construct line from two points

The most basic operation with a line is to construct it from two points. The details of the construction are shown in Fig. 1↓. The direction vector is

ŝ = (r₁ − r₂)/(| r₁ − r₂|).

Note that the direction of ŝ is ambiguous depending on the ordering of the two points. But this is also the case with alternate definitions and the user needs to take this into account. The end of the normal vector n is on the line so n = r₁ + t₀ŝ. Since n is perpendicular to ŝ

n⋅ŝ = 0 = r₁⋅ŝ + t₀.

Solving, we see that t₀ = − r₁⋅ŝ. With this value we can compute the line n vector as r₁ + t₀ŝ.

Construct line as intersection of two planes

I specify a plane as two parameters: a unit vector p̂ perpendicular to the plane and the distance of the perpendicular to the plane p. I use two parameters because just using the perpendicular vector cannot represent a plane passing through the origin. I also have a convention that the p parameter is positive. If the computation results in a negative number, we can use its absolute value and negatep̂.

The problem is to compute the parameters of the line n and ŝ from the two planes, p̂₁, p₁ and p̂₂, p₂ . First, since the line is in both planes, it is perpendicular to both p̂ vectors so it is parallel to their cross product

ŝ = (p̂₁ × p̂₂)/(|p̂₁ × p̂₂|).

Also, n is in the plane spanned by the p̂ vectors

n = k₁p̂₁ + k₂p̂₂.

The end of the n vector is in both planes so

n⋅p̂₁ = p₁ = k₁ + k₂p₁₂ n⋅p̂₂ = p₂ = k₁p₁₂ + k₂

where p₁₂ = p̂₁⋅p̂₂. Solving these two simultaneous equations for k₁ and k₂

k₁ = (p₁ − p₂p₁₂)/(1 − p²₁₂) k₂ = ( − p₁p₁₂ + p₂)/(1 − p²₁₂)

Notice that if p̂₁ = p̂₂, the planes are parallel, p₁₂ = 1, and the equations break down.

Figure 1 Construct Line from two points. This shows examples of the construction diagram for two different cases. In the left panel, the n vector is between the two points, while in the right it is to one side.

Point at intersection of two lines

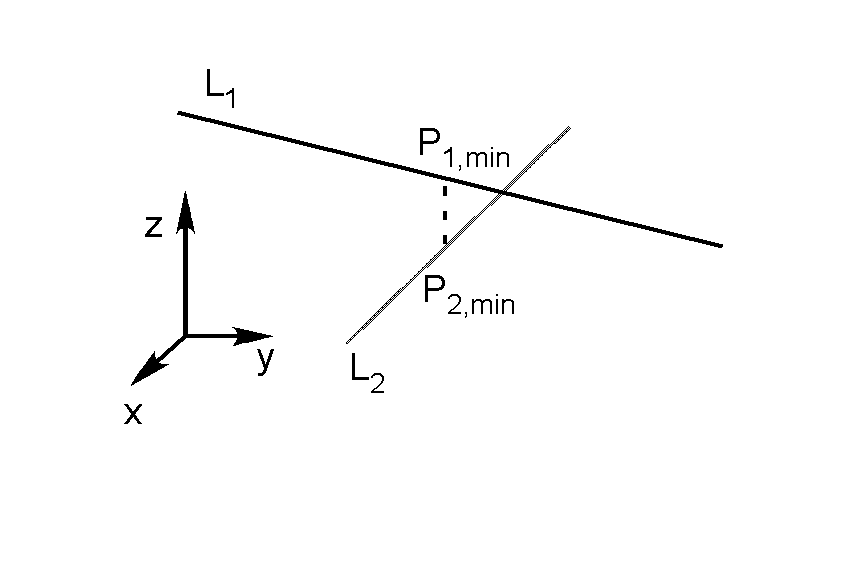
Unlike the 2D case, lines in three dimensions usually do not intersect. Even if they do, the computation of the intersection point is subject to round off errors. I get around this by defining the intersection as the midpoint of the shortest line segment between the two lines as in Fig. 2↓. This is still undefined if the lines are parallel but that is to be expected. The general formula for points on the lines is P_i = n_i + t_iŝ_i i = 1, 2. The line segment between points on the lines is v = P₁ − P₂ = δn + t₁ŝ₁ − t₂ŝ₂ where δn = n₁ − n₂. The minimum length segment is perpendicular to both lines

v⋅ŝ₁ = 0 = δn⋅ŝ₁ + t₁ − t₂s₁₂ v⋅ŝ₂ = 0 = δn⋅ŝ₂ + t₁s₁₂ − t₂

where s₁₂ = ŝ₁⋅ŝ₂. Solving the equations

t_1, min = ( − d₁ + d₂s₁₂)/(1 − s²₁₂) t_2, min = ( − d₁s₁₂ + d₂)/(1 − s²₁₂)

where d_i = δn⋅ŝ_i i = 1, 2. Substituting these in the general formula for points on a line gives the points on each line closest to the other, P_1, min, P_2, min. The “intersection” point is then

P_intersect = 0.5( P_1, min + P_2, min).

The user can check the length of the line segment [P_1, min, P_2, min] to decide whether this is an intersection. The formula gives the correct point for the intersection in two dimensions.

Figure 2 Intersection of two lines. This is defined as the center point of the shortest line segment between the two lines.

Distance of point from line

A common operation is to compute the perpendicular distance of a point from a line. Suppose the point is at P. A point on the line is P_L = n + tŝ. The vector joining the original point and a point on the line is v = P − P_L. This vector is perpendicular to the line if

v⋅ŝ = 0 = P⋅ŝ − t_perp

Solving, t_perp = P⋅ŝ and the distance is

d = |P − n − t_perpŝ|.

Construct a plane from a point and a line

From elementary geometry a plane can be defined from a line and a point outside the line. The line segment from the point to the line n vector, P − n, is in the plane as is the line ŝ vector. Therefore P_perp = (P − n) × ŝ is perpendicular to the plane and the plane normal vector is

p̂ = (P_perp)/(|P_perp|)

The line n vector is in the plane so the plane distance parameter is p = n⋅p̂.

Intersection of a line and a plane

Another common operation is to find the intersection point of a line and a plane. As usual, a point on the line is P_L = n + tŝ. At the intersection, P_L⋅p̂ = p so

(n + t_intersectŝ)⋅p̂ = p

and

t_intersect = (p − n⋅p̂)/(ŝ⋅p̂).

Last edited Aug. 17, 2011

Linking is allowed but reposting or mirroring is expressly forbidden.

References

[1] Philip Schneider, David H. Eberly: Geometric Tools for Computer Graphics. Morgan Kaufmann, 2002.